Polytopes

This page looks at the question: How can we generalize the 5 Platonic Solids into 4 and more dimensions?

The next in the series: a point, a line, a square, a cube is the of 4 and more dimensions.
The next in the series: a point, a line, an equilateral triangle, a tetrahedron is a simplex of 4 or more dimensions.

What are these and are there other regular shapes in more then 3 dimensions?

Contents of this page

How to show higher-dimensional shapes on a flat screen

Names

If objects with straight edges in 2D are called polygons and solid shapes in 3D are called polyhedrons then we use the term polytope for a straight-edged shape in any dimension higher than 3.
We usually abbreviate 2 dimensions to 2D, 3 dimensions to 3D, 4D and so on. We have points in 0D, lines and polygons are in 2D and polyhedrons and solid shapes are in 3D. Shapes in higher-dimensions are often called polytopes.

Representing higher-dimensional shapes on a flat surface

Here we are only able to represent 3D shapes in a flat screen (in 2D). We can try to imagine then in 3 dimensions by animating them or by showing s=different projections of them onto a flat surface.

Coordinates

We can also generalise coordinates to describe points, lines, 2D shapes etc from a flat 2D x-y coordinate system (x,y) to three diimensions with (x,y,z) where z is the distance of a point "above" the (x,y) plan4 on the page.
So 4 dimensions is just (x,y,z,w) and 5 is (x,y,z,w,p) and so on. The coordinates will be numbers, representing the distance from an origin point which is (0,0) is 2D, (0,0,0) is 3D, (0,0,0,0) in 4D and so on.

Distances

The distance from the origin to a point (x,y) in 2 dimensions is √x² + y² and the distance between (a,b) and (x,y) is √(x−a)² + (y−b)² by moving the point (x,y) so that (a,b) becomes the origin.
In 3 dimensions the length of a line from the origin (0,0,0) to (x,y,z) is √x² + y² + z² and this gives the pattern for the length of the line from the origin to the 4 dimensional point (x,y,z,w) as √x² + y² + z² + w². This is called the Euclidean distance and is the square-root of the sum of the squares of the coordinates. It applies to 4 and higher dimensions.

The Schläfli symbol

For a 2D regular polygon of p sides: the Schläfli symbol is {p}. So a square is {4} and a regular pentagon is {5}.
For a 3D regular solid: where at each vertex we have q regular polygons {p}, the symbol is {p,q}.
For instance the cube has 3 square (faces) meeting at each corner (vertex) so its symbol is {4,3}.
for 4D: the symbol {p,q,r} means there are r {p,q} (3D) solids meeting at each vertex.
for higher dimensions: There are n-1 numbers in the symbol for an n dimensional polytope.
There are only 3 classes of regular polytopes that extend to all higher dimensions.
the simplexes which generalise the tetrahedron, with symbol {3,3,...,3};
the hypercubes which generalise the cube, with symbols {4,3,3,...,3};
the cross-polytopes which generalise the octahedron, with symbol {3,3,...,3,4}.

A useful feature of this notation is that if we reverse the Schläfli symbol for a polytope we get the symbol for its dual. If we get the same symbol, the polytope is self-dual. So in 3D a cube is {4,3} and an octahedron is {3,4} (4 equilateral triangles at each vertex) so they are duals. The tetrahedron {3,3} with 3 equilateral triangles meeting at each vertex is its own dual.

We will look at each of these in the following sections.

Cubes and Hypercubes

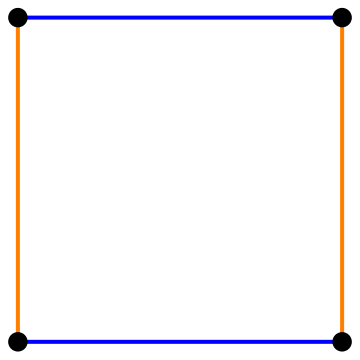
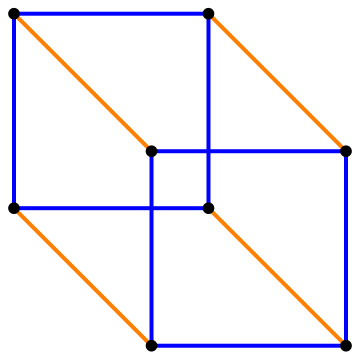
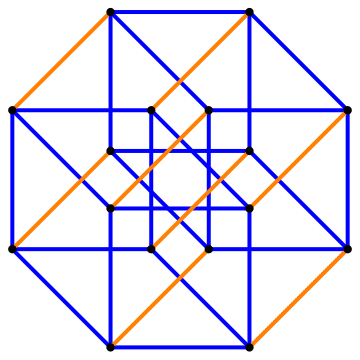
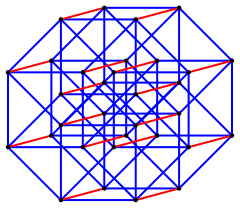
Perhaps the easiest to undertand are the hypercubes.
In the series we have a point (0D), a line (1D), a square (2D), a cube (3D) and then we have hypercubes, also called tesseracts.

How to generate hypercubes

Each shape in the series point, line, square, cube is derived from the previous one by including a a copy of it. We can imagine that all the points leave a trail from the original to the copy, forming new edges in the new dimension.

Shape	∙
Dimension	0	1	2	3	4	5

To go from (a projection of) one dimension to the next, copy the projection moving it along a new direction (shown in orange above); then join the points to their copies as the (projected) edges of the new dimension .

The number of points will double each time we go to the next dimension.
From 1 point with dimension 0, 2 points ( a line) in 1 dimension, 4 points for a 2D square, ....
So there are 2ⁿ vertices of a hypercube in dimension n.
The number of edges will double and there are extra edges between the points and their copies.

The square faces and cubes are more difficult to see but the formula is as follows:
we have taken two copies of the previous dimensional object so we double the number of faces (cubes, ...) etc. But we also have made new edges, faces, etc equal to the number of 1-dimension-smaller objects, so the extra faces are made from each edge in the smaller dimension, the extra cubes are made form each face in the smaller dimension and so on.
So from a cube with 8 points and 6 square faces and 12 edges to the next dimension, we find the faces are 2×6 faces and 12 square faces from the 12 edges: a total of 24 square faces in the 4D hypercube.
Similarly, the number of edges in the 4D hypercube cube is twice 12 edges from the two cubes plus 8 more where the 8 points of the cube now become edge in the 4D version: a total of 24+8=32 edges.

Shape

Dim

points

edges

faces

cubes

Point

Line

Square

Cube

4D Hypercube

5D Hypercube

6D Hypercube

192

240

160

7D Hypercube

128

448

672

560

280

8D Hypercube

256

1024

1792

1120

448

112

9D Hypercube

512

2304

4608

5376

4032

2016

672

144

n D

2ⁿ

n 2^n-1

(	n	)	2^n-2
	2

(	n	)	2^n-3
	3

(	n	)	2^n-4
	4

(	n	)	2^n-5
	5

(	n	)	2^n-6
	6

(	n	)	2^n-7
	7

OEIS:

A001789

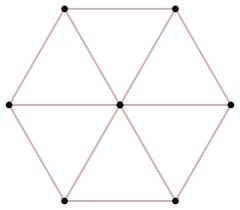
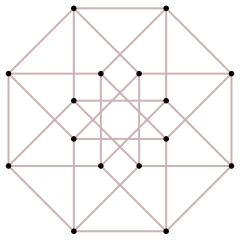
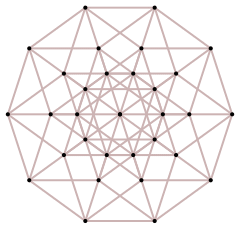
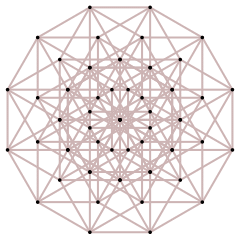
Here is a symmetric form of the hypercubes. For odd n, the projection is looking along a largest "diagonal" (joining two opposite points) across the centre:

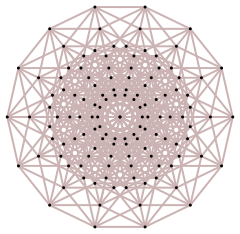Shape ∙ line square cubeReg 4D cubeReg 5D cubeReg 6D cubeReg 7D cubeReg

Dimension 0 1 2 3 4 5 6 7

Coordinates of a hypercube

One way to describe the vertices of a 3D cube is to take all the points with 0 or 1 in each dimension.
A cube is thus (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1)
Notice that these are just the 8 3-bit binary numbers in order. This shows there are 2³ = 8 of them.
We can put a 0 in fromt on them all as the fourth coordinate and also a 1 in front of the all and get twice as many points for the next polytope (hypercube) in the next dimension. In practice this is taking a copy of the cube and moving it one unit in the new dimension.
Of course, on the 2D flat page, this is projected as a copy of the points but in a new (2D) direction with each new point joined to its original.

An alternative set of coordinates is +1 or −1 in all dimensions, for example:

a square is has (x,y) points (-1,-1), (-1,1), (1,-1), (1,1)
a cube has 8 points, 4 of them making a square with z-coordinate -1 :
(-1, -1, -1), (-1, 1, -1), (1, -1, -1), (1, 1, -1)
and the other 4 with the square and a z-coordinate of 1:
(-1, -1, 1), (-1, 1, 1), (1, -1, 1), (1, 1, 1)
repeat this process by adding on the new dimension's coordinate in the same way, extending the polytope in the previous dimension
this even works for the square if we start with a line on a single axis with two points, one at -1 and one at 1.

Tetrahedron and the Simplex

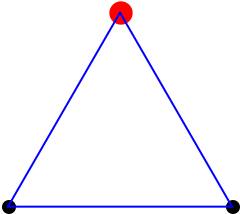
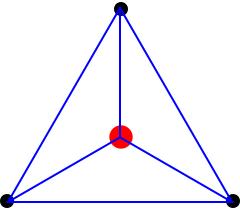
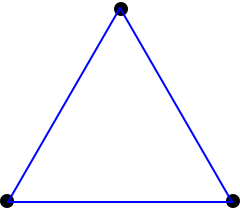
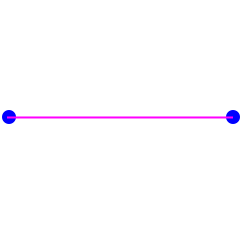
This sequence of polytopes is based on the euilateral triangle.
The sequence of this section is point (0D), line (1D), equilateral traingle (2D), tetrahedron (3D), ... . A common name for a higher-dimensional shape in this series is a simplex, the plural of which is simplexes or simplices. Coexeter calls these α_n.
Strictly, we want all the edges to be the same length but first we just see how to construct these without the same-length-sides condition, using unit lengths in each of the n dimensions.

How to generate tetrahedrons in higher dimensions

In 3D we form the tetrahedron by adding in one new point in the new (third) dimension and joining it to each of the current points in the previous 2 dimensions with a unit length line.
This a line (1D) becomes an equilateral triangle in 2D which, in turn, becomes a tetrahedron in 3D.

Coordinates

Without insisting the lines in a simplex are all of the same length, we can use coordinates (0,0), (1,0), (0,1) for a triangle in 2D
(0,0,0), (1,0,0), (0,1,0), (0,0,1) for a tetrahedron in 3D
We have places the previous shape on the 0 "plane" of the new dimension and added a new point "above the origin" at distance 1 in the new dimension. The process is thus to append 0 as the new dimensions coorsdinate for all current points and then add in a new point with 0s in all dimensions except the new one which is 1 as its coordinate.
The triangle (0,0), (1,0), (0,1) becomes (0,0, 0), (1,0, 0), (0,1, 0) together with the new point (0,0,1).
For 4D we therefore have vertices at (0,0,0, 0), (1,0,0, 0), (0,1,0, 0), (0,0,1, 0) and (0,0,0,1) in 4D.
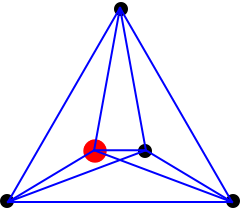
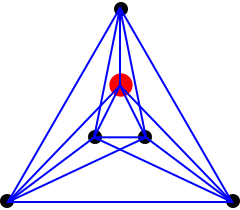
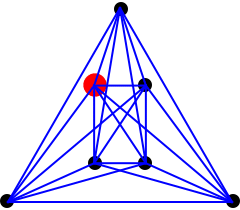
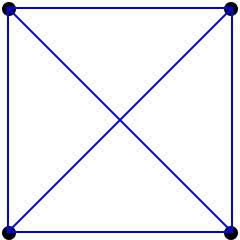
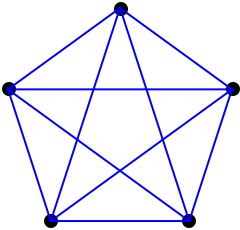
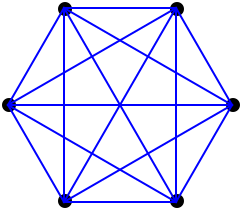
A simplex in n dimensions has n+1 points: the origin and points with a single 1 in each dimension, other coordinates being 0.

Shape	∙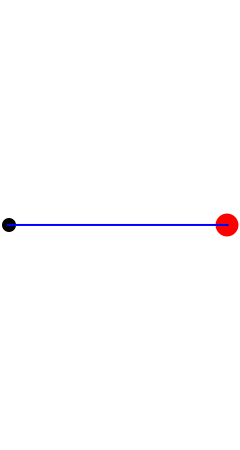
K(n)	∙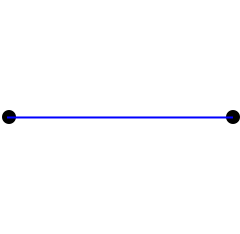
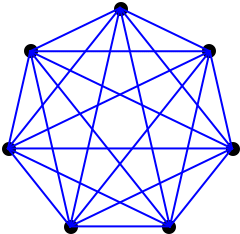Dimension	0	1	2	3	4	5	6	n
#Vertices	1	2	3	4	5	6	7	n+1
#edges(1D)	0	1	3	6	10	15	21	A000217
#faces(2D)	0	0	1	4	10	20	35	A000292
#(3D)	0	0	0	1	5	15	35	A000322
#(4D)	0	0	0	0	1	6	21	A000389

A diagram of n points where each is joined to all the others by a line (as here) is called a complete network denoted by K(n) when it has n vertices (nodes). They have a nice symmetrical representation as follows where all the vertices are equally spaced around a circle.
You will probably have noticed how the table above is just Pascal's triangle but left-to-right instead of top-to-bottom and without its first row of ones. This makes it easy to extend to more dimensions.

In n dimensions we put 3 of the previous dimension's simplexes at each on the n+1 vertices, so its Schlälfli symbol {3,3,3} for 4 dimenions, {3,3,3,3} for 5 dimensions and so on.

The simplexes with equal-length sides

A nice exercise is to compute the coordinates of the 3D and higher simplexes with unit length sides based on the coordinates of the previous dimension.
For the 2D simplex we want a new point (x,y) in 2D space to be distance 1 from both (0,0) and (0,1): we need to solve simultaneously

x² + y² = 1
(x−1)² + y² = 1

which makes the third point of the triangle to be (	1	, ±	√3	)
	2		2

If we use both points, we have a square and this leads us into the octahedron which we look at in more detail in the next section.
If we choose only the positive coordinates, we have the equilateral triangle that we want and this leads to the tetrahedron and the other simplexes.

Now for the tetrahedron, to find the coordinates of a fourth point in 3D and x-, y- and z-axes, we use the previous three points we found for x and y values and find a new point (x,y,z) a unit distance from all three:

x² + y² + z²= 1
(x − 1)² + y² + z² = 1
(x − 1/2)² + (y - (√3)/2)² + z² = 1

The solutions are:

x =	1	, y=	1	, z = ±	√2
	2		2√3		√3

.
Again we will find a positive and a negative value for z so we choose just the positive value.
We will then have the coordinates of the 4 points of the tetrahedron with all sides of length 1:

(0,0,0) (1,0,0) (	1	,	√3	,0) (	1	,	1	,	√2	)
	2		2		2		2√3		√3

By the time we reach dimension 6 the pattern in the coordinates is much easier to spot:

Axes:	(	x	,	y	,	z	,	dim4	,	dim5	,	dim6	)
point 1:	(	0	,	0	,	0	,	0	,	0	,	0	)
point 2:	(	1	,	0	,	0	,	0	,	0	,	0	)
point 3:	(	1	,	√3	,	0	,	0	,	0	,	0	)
point 3:	(	2	,	√2	,	0	,	0	,	0	,	0	)
point 4:	(	1	,	1	,	√2	,	0	,	0	,	0	)
point 4:	(	2	,	2√3	,	√3	,	0	,	0	,	0	)
point 5:	(	1	,	1	,	1	,	√5	,	0	,	0	)
point 5:	(	2	,	2√3	,	2√6	,	√8	,	0	,	0	)
point 6:	(	1	,	1	,	1	,	1	,	√3	,	0	)
point 6:	(	2	,	2√3	,	2√6	,	2√10	,	√5	,	0	)
point 7:	(	1	,	1	,	1	,	1	,	1	,	√7	)
point 7:	(	2	,	2√3	,	2√6	,	2√10	,	2√15	,	√12	)

Can you spot the pattern?

After the origin (point 1), and the point at x=1 and 0s elsewhere (point 2):
point k(>2) has as its first k-2 coordinates, in order:
1 over twice the square-root of the triangular numbers 1,3,6,10,....

The k-th point has k-1 non-zero coordinates and its final coordinate in dimension (k-1) is
the square-root of (k+1) over the square-root of 2k

At each vertex in the tetrahedron we have 3 equilateral triangles so its Schlälfi symbol is {3,3}.

Octahedrons: the Cross-Polytopes

The next Platonic solid to consider is the octahedron (two square-based pyramids joined by their bases) shown on the right.
All the triangular faces are identical and all its sides are the same length. We form it from a square with its 4 vertices each joined to a point above (in dimension 3) and a point below.
Such shapes are called cross polytopes.

Coordinates

If we define the starting as two points at 1 and −1 on the x axis then we can extend these to the square by adding in two new points with coordinates at +1 and −1 on the y-axis and x=0: (1,0), (-1,0), and two new points (0,1) and (0,−1).
In 3D this becomes a square in the x=y plane with z=0 and two new points (0,0,1) and (0,0,−1).
The coordinates of an octahedron are then: (1,0,0),(-1,0,0), (0,1,0), (0,-1,0) together with (0,0,1) "above" and (0,0,−1) "below".
This process easily extends to more dimensions by using all the n-1 dimensions points with 0 in the new dimension together with (0,0,..0,1) and (0,0,...,0,−1) in the new n-th dimension. In this way we have two points for each dimension with all edges the same length . But note that edges are only between certain pairs of points because the two new points in each dimension are not joined by an edge.
There are 4 points for the square, 6 points for the octahedron, 8 points for the 4D cross polytope and so on giving 2n vertices for the cross polytope in n dimensions.
The 4D cross polytope is called the 16 cell as it has 16 octahedrons.

Visualisation

If we arrange the vertices around a circle we have the following vusualisations:

Shape	∙
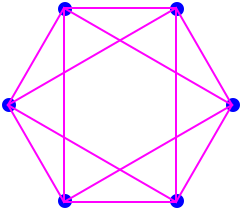
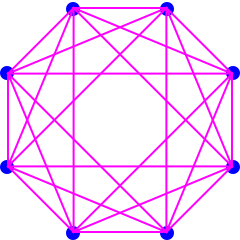
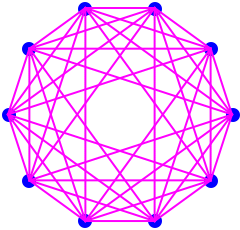
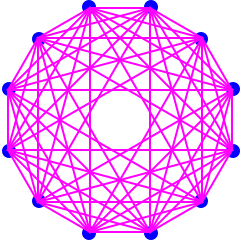
Dimension	0	1	2	3	4	5	6	n
#Vertices	1	2	4	6	8	10	12	2n:A005843
#edges(1D)	0	1	4	12	24	40	60	A046092
#faces(2D)	0	0	1	8	32	80	160

These numbers are closely related to those of the tetrahedron (simplex) above.
After the first 1 on each line we have:
the number of vertices is 2×(# vertices(K(n));
the number of 1d "edges" is 4×#edges(K(n));
the number of 2d "faces" is 8×#2d(K(n));
etc.

The unit-length cross-polytopes

If we proceed as we did for the simplexes in the previous section, we can now always include both values for the new dimension and so have all-edges-of-equal-length cross-polytopes.

The 24-cell

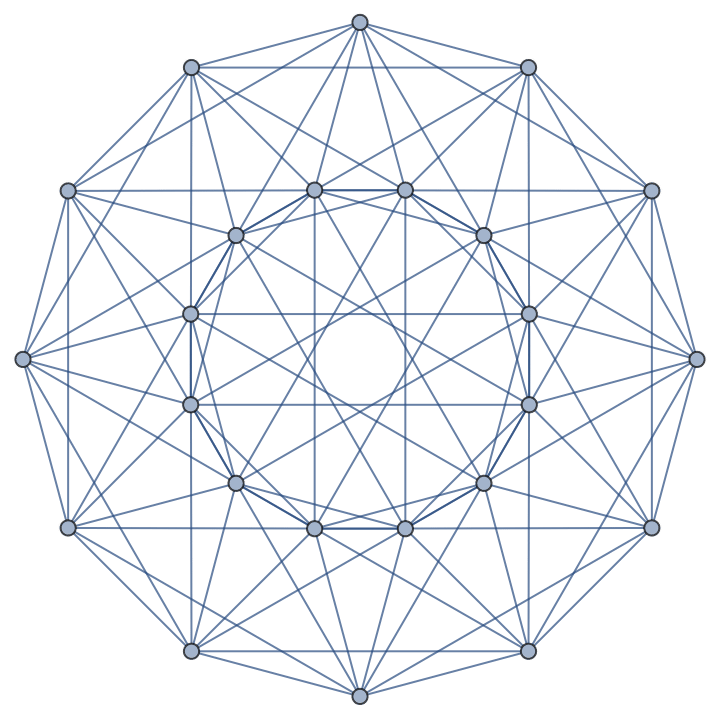All the three types above, the hypercubes, the simplexes and the cross polytopes exist in all dimensions. There is one other polytope that exists only in 4D , called the 24-cell.
Its Schlälfli symbol is {3,4,3}.
It has 24 vertices, 96 edges and 96 triangular 2D "faces" and 24 3D octahedrons.

Coordinates

There are 24 vertices in the 24-cell with edges of length √2:

(±1, ±1, 0, 0); (±1, 0, ±1, 0); (±1, 0, 0, ±1); (0, ±1, ±1, 0); (0, ±1, 0, ±1); (0, 0, ±1, ±1)

A 24-cell with all edges of length 1 is given by the coordinates

(±1, 0, 0, 0); (0, ±1, 0, 0); (0, 0, ±1, 0); (0, 0, 0, ±1);
(±½, ±½, ±½, ±½)

The first set is 8 vertices with either +1 or −1 on one of the 4 axes and 0 as its other 3 components.
Those at ½ on all 4 axes occur as all 16 combinations of + and − signs.

The 60-cell and the 120-cell

We could ask if there are 4d and higher dimension analogues oif the icosahedron and the dodecahedron. The answer is yes, but for 4D only. They are called the 120-cell for the dodecahedron and the 600-cell for the icosahedron and they are, like their 3D counterparts, duals of each other.

	120-cell	600-cell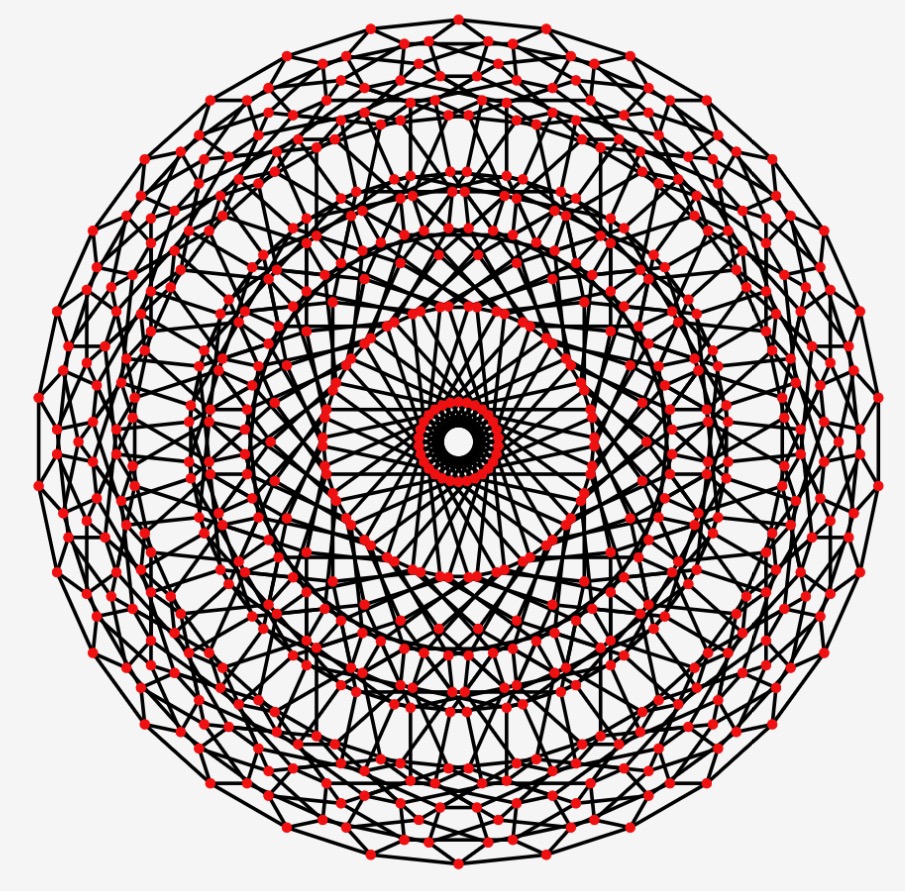

Schlälfli	{5,3,3}	{3,3,5}
#V	600	120
#E	1200	720
at each V	4 dodecahedrons	20 icosahedrons
in total	120 dodecahedrons	600 icosahedrons
#(2d)F	720 pentagons	1200 equi-triangles

References

Regular Polytopes H S M Coxeter, (1973, third edition, Dover)
This is the classic reference book, with much information in a fairly compact form.
n-Dimensional Enrichment for Further Mathematicians M Griffiths, Math Gaz (2005) pp 409-416 JSTOR
A good paper on introducing the idea of shapes in 4 and more dimensions to 14-16 year old students in a maths class
Further Forays into N Dimensions D Quadling, Math Gaz (2007) pp 462-468 JSTOR
A companion article to Martin Griffiths article above
Shadows of Four-dimensional polytopes, B L Chilton, Maths Mag (1971) pages 269-273 JSTOR