Fibonacci and Golden Ratio Formulae

Here are almost 300 formula involving the Fibonacci numbers and the golden ratio together with the Lucas numbers and the General Fibonacci series (the G series). This forms a major reference page for Ron Knott's Fibonacci Web site (http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fib.html) where there are many more details and explanations with applications, puzzles and investigations aimed at secondary school students and teachers as well as interested mathematical enthusiasts.
Note that it is easy to search for a named formula on this page since it is an HTML page and the formulae are not images. In your browser main menu, under the Edit menu look for Find... and type Vajda-N or Dunlap-N for the relevant formula. Full references are at the foot of this document.

A companion page on Linear Recurrences and their generating Functions for Fibonacci Numbers, Continued Fraction convergents, Pythagorean triples and other series of numbers.

The calculators and Contents sections on this page require JavaScript but you appear to have switched JavaScript off (it is disabled). Please go to the Preferences for this browser and enable it if you want to use the calculators, then Reload this page.
Contents of this page

Definitions and Notation

Beware of different golden ratio symbols used by different authors!
Where a formula below (or a simple re-arrangement of it) occurs in either Vajda or Dunlap's book, the reference number they use is given here. Dunlap's formulae are listed in his Appendix A3. Hoggatt's formula are from his "Fibonacci and Lucas Numbers" booklet. Full bibliographic details are at the end of this page in the References section.
As used hereVajdaDunlapKnuthDefinitionDescription
Phi
Φ		 τ τφ, α
√5 + 1
2
= 1.6180339... 		Koshy uses α (page 78)
phi
φ		 −σ−φ−β
√5 − 1
2
= 0.6180339... 		Koshy uses −β (page 78)
abs(x)
|x|		|x||x||x|abs(x) = x if x≥0;
abs(x) = −x if x<0		the absolute value of a number, its magnitude; ignore the sign;
floor(x)
⌊x⌋ 		[x]trunc(x), not used for x<0 ⌊x⌋ the nearest integer ≤ x. When x>0, this is "the integer part of x" or "truncate x" i.e. delete any fractional part after the decimal point.
3=floor(3)=floor(3.1)=floor(3.9), -4=floor(-4)=floor(-3.1)=floor(-3.9)
round(x)
[x]
[ x +  1 ]
--
2
trunc(x + 1/2)   the nearest integer to x; trunc(x+0.5) 3=round(3)=round(3.1), 4=round(3.9),
-4=round(-4)=round(-3.9), -3=round(-3.1)
4=round(3.5), -3=round(-3.5)
ceil(x)
⌈x⌉ 		-- ⌈x⌉ the nearest integer ≥ x. 3=ceil(3), 4=ceil(3.1)=ceil(3.9), -3=ceil(-3)=ceil(-3.1)=ceil(-3.9)
fract(x)
frac(x)		-- x mod 1 x − floor(x) the fractional part of x, i.e. the part of abs(x) after the decimal point
(n
r		)
(n
r		)
(n
r		)
(n
r		)
n!
r! (n − r)!
 nCr
n choose r;
the element in row n column r of Pascal's Triangle
the coefficient of xr in (1+x)n
the number of ways of choosing r objects from a set of n different objects.
n≥0 and r≥0 (otherwise value is 0)

Fibonacci-type series with the rule S(i)=S(i-1)+S(i-2) for all integers i:
i...−6−5−4−3−2−10123456...
Fibonacci
F(i)		...−85−32−110112358...
Lucas
L(i)		...18−117−43−1213471118...
General Fib
G(a,b,i)		...13a−8b−8a+5b5a−3b−3a+2b2a−b−a+baba+ba+2b2a+3b3a+5b5a+8b...
FormulaRefsComments
F(0) = 0, F(1) = 1,
F(n+2) = F(n + 1) + F(n)		-Definition of the Fibonacci series
F(−n) = (−1)n + 1 F(n)Vajda-2, Dunlap-5 Extending the Fibonacci series 'backwards'
L(0) = 2, L(1) = 1,
L(n + 2) = L(n + 1) + L(n)		-Definition of the Lucas series
L(−n) = (−1)n L(n)Vajda-4, Dunlap-6Extending the Lucas series 'backwards'
G(n + 2) = G(n + 1) + G(n)Vajda-3, Dunlap-4Definition of the Generalised Fibonacci series, G(0) and G(1) needed
Phi = 1.618... =  
√5 + 1
2
 Dunlap-63 Phi and −phi are the roots of x2 = x + 1
phi = 0.618... = 
√5 − 1
2
 Dunlap-65 Beware! Dunlap occasionally uses φ to represent our phi = 0.61803.., but more frequently he uses φ to represent −0.61803.. !

Linear Formulae

Linear relationships involve only sums or differences of Fibonacci numbers or Lucas numbers or their multiples.

Linear Sums of Fibonacci numbers

F(n + 2) + F(n) + F(n − 2) = 4 F(n) B&Q(2003)-Identity 18
F(n + 2 ) + F(n) = L(n + 1)by Definition of L(n), Vajda-6, Hoggatt-I8,
B&Q(2003) Identity 32, Dunlap-14, Koshy-5.14
F(n + 2) − F(n) = F(n + 1) by Definition of F(n)
F(n + 3) + F(n) = 2 F(n + 2) B&Q(2003)-Identity 16
F(n + 3) − F(n) = 2 F(n + 1)-
F(n + 4) + F(n) = 3 F(n + 2) B&Q(2003)-Identity 17
F(n + 2) + F(n − 2) = 3 F(n) B&Q(2003)-Identity 7
F(n + 2) − F(n − 2) = L(n) Hoggatt-I14
F(n + 4) − F(n) = L(n + 2)-
F(n + 5) + F(n) = F(n + 2) + L(n + 3)-
F(n + 5) − F(n) = L(n + 2) + F(n + 3)-
F(n + 6) + F(n) = 2 L(n + 3)-
F(n + 6) − F(n) = 4 F(n + 3)-
F(n) + 2 F(n − 1) = L(n)(Dunlap-32), B&Q(2003) Identity 50
F(n + 2) − F(n − 2) = L(n)Vajda-7a, Dunlap-15,
Koshy-5.15
F(n + 3) − 2 F(n) = L(n)possible correction for Dunlap-31
F(n + 2) − F(n) + F(n − 1) = L(n)possible correction for Dunlap-31
F(n) + F(n + 1) + F(n + 2) + F(n + 3) = L(n + 3)C Hyson(*)

Linear Sums of Lucas numbers

L(n − 1) + L(n + 1) = 5 F(n)Vajda-5, Dunlap-13,
Koshy-5.16,
B&Q(2003)-Identity 34, Hoggatt-I9
L(n) + L(n + 3) = 2 L(n + 2)-
L(n) + L(n + 4) = 3 L(n + 2)-
2 L(n) + L(n + 1) = 5 F(n + 1)B&Q(2003)-Identity 52
L(n + 2) − L(n − 2) = 5 F(n)-
L(n + 3) − 2 L(n) = 5 F(n)-

Linear Sum of a Fibonacci and a Lucas number

F(n) + L(n) = 2 F(n + 1)Vajda-7b, Dunlap-16,
B&Q-Identity 51
L(n) + 5 F(n) = 2 L(n + 1)-
3 F(n) + L(n) = 2 F(n + 2)Vajda-26, Dunlap-28
3 L(n) + 5 F(n) = 2 L(n + 2)Vajda-27, Dunlap-29

Golden Ratio Formulae

Defining relations: The roots of x2 = x + 1 are
Φ = Phi = 1 + √5= 1.61803398874989484820458683436...
2
−φ = −phi = 1 − √5 = −0.61803398874989484820458683436...
2

Basic Phi Formulae

Phi phi = 1Vajda page 51(3), Dunlap-65
Phi + phi = √5-
Phi / phi = Phi + 1-
phi / Phi = 1 − phi-
Phi = phi + 1 = √5 − phi-
phi = Phi − 1 = √5 − Phi -
Phi2 = Phi + 1Vajda page 51(4), Dunlap-64
Phin+2 = Phin+1 + Phin ∀n∈ℤPhin× Vajda page 51(4)
phi2 = 1 − phiVajda page 51(4), Dunlap-64
phin+2 = phin − phin+1 ∀n∈ℤphin×Vajda page 51(4)
phin = phin+1 + phin+2 ∀n∈ℤfrom line above

Golden Ratio with Fibonacci and Lucas

Phi = √5 + 1 = 1 = phi + 1; phi = √5 −1 = 1 = Phi −1
2phi2Phi
F(n) =   Phin − (−phi)n
√5
"Binet's" Formula
De Moivre(1718), Binet(1843), Lamé(1844),
Vajda-58, Dunlap-69, Hoggatt-page 11, B&Q(2003)-Identity 240
L(n) = Phin + (−phi)n Vajda-59, Dunlap-70, B&Q(2003)-Identity 241
Phin = Phi F(n) + F(n−1) Vajda-50a, Rabinowitz-28, B&Q(2003)-Corrolary 33
Phin = F(n+1) + F(n) phiRabinowitz-28, B&Q(2003)-Corollary 33
Phin = L(n) + F(n)√5
2
 Vajda-50b, Rabinowitz-25, B&Q(2003)-Identity 242,
I Ruggles (1963) FQ 1.2 pg 80
(−phi)n = L(n) − F(n)√5
2
 Vajda-50c, I Ruggles (1963) FQ 1.2 pg 80,
Rabinowitz-25, B&Q(2003)-Identity 243
(−phi)n = −phi F(n) + F(n−1)Rabinowitz-28
(−phi)n = F(n+1) − Phi F(n)Vajda-103b, Dunlap-75
√5 Phin = Phi L(n) + L(n−1)-
√5 (−phi)n = phi L(n) − L(n−1)-

Some useful special cases

These follow simply from Vajda-50a and the basic definitions of Phi above.
Phi + 2 = √5 Phi
Phi2 + 1 = 2 + Phi = 5 + √5 = √5 Phi
2
Phi3 + 1 = 2 + 2 Phi = 2 Phi2 = 3 + √5
Phi6 = 4 Phi3 + 1 = 5 + 8 Phi = 9 + 4√5
Phi8 = 7 Phi4 − 1 = 13 + 21 Phi

Golden Ratio with Fibonacci and Lucas - Approximations

Lim
n→∞
  
F( n+1 )
F( n )
  = Phi
 Vajda-101
Lim
n→∞
  
F( n+m )
F( n )
  = Phim
 Vajda-101a
F(n) = round( Phin ) ,if n≥0
√5
Vajda-62, Dunlap-71 corrected, B&Q(2003)-Identity 240 Corollary 30
L(n) = round(Phin),if n≥2Vajda-63, Dunlap-72, B&Q(2003)-Corollary 35
F(−n) = round (
−(−phi)−n
√5
 ) ,if n≥0
-
L(−n) = round( (−phi)−n ), n≥2-
F(n + 1) = round(Phi F(n)),if n≥2Vajda-64, Dunlap-73
L(n + 1) = round(Phi L(n)),if n≥4Vajda-65, Dunlap-74
fract( F(2n) phi ) = 1 − phi2nKnuth vol 1, Ex 1.2.8 Qu 31 with ψ=phi
fract( F(2n+1) phi ) = phi2n+1Knuth vol 1, Ex 1.2.8 Qu 31

Fibonacci and Lucas Factors

F(nk) is a multiple of F(n)
F(nk) ≡ 0 (mod F(k)) 		B&Q(2003)-Theorem 1, Vajda Theorem I page 82
gcd(F(m),F(n)) = F(gcd(m,n))Lucas (1878)
B&Q(2003)-Theorem 6,Vajda Theorem II page 83
F(mn+r) ≡ ± F(r) (mod F(n) )Knuth Vol 1 Ex 1.2.8 Qu. 32, Vajda page 86
gcd(L(m),L(n)) = L(gcd(m,n)),
if both L(m)/gcd(L(m),L(n)) and
L(n)/gcd(L(m),L(n)) are odd integers		Vajda page 86
L(mn+r) ≡ ± L(r) (mod L(n) ) (Vajda page 87)
F(m q) = F(m)
q
∑
j = 1
F(m - 1) j-1 F( m(q - j) + 1 ) 
 B&Q(2003)-Theorem 2
F(kt)
F(t)
  =
(k−3)/2
∑
i = 0
(−1)itL( (k−2i−1)t )
   + (−1)(k−1)t/2 for ODD k ≥ 3
Vajda-85
F(kt)
F(t)
  =
k/2−1
∑
i = 0
(−1)itL( (k−2i−1)t )
    for EVEN k ≥ 2
Vajda-86
L(kt)
L(t)
  =
(k−3)/2
∑
i = 0
(−1)i(t+1)L( (k−2i−1)t )
  + (−1)(k−1)(t+1)/2    for ODD k ≥ 3
Vajda-87
L(t) is not a factor of L(kt) for even k
F(kt)
L(t)
  =
k/2−1
∑
i = 0
(−1)i(t+1)F( (k−2i−1)t )
    for EVEN k ≥ 2
 Vajda-88
L(t) is not a factor of F(kt) for odd k and t≥3
p prime ⇒ p is a factor of L(p) − 1 B&Q(2003) Identity 228
p prime ⇒ p is a factor of L(2p) − 3 B&Q(2003) Identity 229

Order 2 Formulae

Order 2 means these formulae have terms involving the product of at most 2 Fibonacci or Lucas numbers.

Fibonacci numbers

F(2n) = F(n + 1)2 − F(n − 1)2Lucas(1878), B&Q(2003)-Identity 14, Hoggatt-I10
F(2n) = F(n) ( F(n+1) + F(n−1) )Vajda-13, Hoggatt-I7,
Koshy-5.13,
B&Q(2003)-Identity 33
with Vajda-6
F(2n) = F(n) (2F(n+1) − F(n)) simple alternative to Vajda-13
F(2n+1) = F(n + 1)2 + F(n)2Vajda-11, Dunlap-7, Lucas(1878), B&Q(2003)-Identity 13, Hoggatt-I11
F(n+2)2 + F(n)2 = 3 F(n + 1)2 − 2 (−1)nV E Hoggatt B-208 FQ 9 (1971) pg 217.
F(n+3)2 + F(n)2 = 2 ( F(n+1)2 + F(n+2)2 )B&Q(2003)-Identity 30
F(n + k + 1)2 + F(n − k)2 = F(2k + 1)F(2n + 1)Sharpe(1965), a generalization of Vajda-11,Dunlap-7
Melham(1999)
F(n + k)2 + F(n − k)2 =F(n + k −2)F(n + k + 1) + F(2k − 1)F(2n − 1)Sharpe (1965)
F(n + 1)2 − F(n)2 = F(n + 2) F(n − 1) Vajda-12, Dunlap-8
F(n + k + 1)2 − F(n − k)2 = F(n − k − 1)F(n − k + 2) + F(2 k)F(2n + 2)Sharpe (1965)
F( n+p )2 − F( n−p )2 = F( 2n )F( 2p ) I Ruggles (1963) FQ 1.2 pg 77; Hoggatt-I25, Sharpe (1965)
F(n + 1) F(n − 1) − F(n)2 = (−1)n Cassini's Formula(1680), Simson(1753), Vajda-29, Dunlap-9, Hoggatt-I13
special case of Catalan's Identity with r=1
B&Q(2003)-Identity 8
F(n)2 − F(n + r)F(n − r) = (-1)n-rF(r)2 Catalan's Identity(1879)
F(n)F(m + 1) − F(m)F(n + 1) = (-1)mF(n − m) d'Ocagne's Identity,
special case of Vajda-9 with G=F
F(n + m) = F(n + 1)F(m + 1) − F(n − 1)F(m − 1) B&Q(2003)-Identity 231
F(n + m) = F(m) F(n + 1) + F(m − 1) F(n) alternative to Dunlap-10, B&Q(2003)-Identity 3;
variation of Hansen (1972)
Vorob'ev (1951) pages 9-10 proof, attributed to I S Sominskii
F(n) = F(m) F(n + 1 − m) + F(m − 1) F(n − m) I Ruggles (1963) FQ 1.2 pg 79; Dunlap-10, special case of Vajda-8
F(n) F(n + 1) = F(n − 1) F(n + 2) + (−1)n-1 Vajda-20a special case: i:=1;k:=2;n:=n-1; Hoggatt-I19
F(n + i) F(n + k) − F(n) F(n + i + k) = (−1)n F(i) F(k) Vajda-20a=Vajda-18 (corrected) with G:=H:=F
2 F(n + 1) = F(n) + √(5 F(n)2 + 4(−1)n) F(n+1) from F(n): Problem B-42, S Basin, FQ, 2 (1964) page 329
F(a)F(b) − F(c)F(d)
= (−1)r( F(a − r)F(b − r) − F(c − r)F(d − r) )
a+b=c+d for any integers a,b,c,d,r		 Johnson FQ 42 (2004) B-960 'A Fibonacci Iddentity', solution pg 90
also Johnson-7
Cassini, Catalan and D'Ocagne's Identities
are all special cases of this formula

Lucas numbers

L(n + 2)2 = 3 L(n + 1)2 − L(n)2 + 10(−1)nV E Hoggatt B-208 FQ 9 (1971) pg 217.
L(n + 2) L(n − 1) = L(n + 1)2 − L(n)2from Vajda-17a
L(n + 1)2 + L(n)2 = L(2n) + L(2n + 2)from Vajda-17a
L(n + 1)2 − L(n − 1)2 = L(2n + 1) + L(2n − 1)from Vajda-17a
L(n + 1) L(n − 1) − L(n)2 = −5 (−1)nB&Q(2003)-Identity 60
L(2n) + 2 (−1)n = L(n)2Vajda-17c, Dunlap-12, B&Q(2003)-Identity 36
L(n + m) + (−1)m L(n − m) = L(m) L(n)Vajda-17a, Dunlap-11
(special cases: Hoggatt-I15,I18)
L(4n) + 2 = L(2n)2Hoggatt-I15, special case of Vajda-17a
2 L(n + 1) = L(n) + √5 √(L(n)2 − 4(−1)n) L(n+1) from L(n): Problem B-42, S Basin, FQ 2 (1964) page 329

Fibonacci and Lucas Numbers

F(2n) = F(n) L(n)Vajda-13, Hoggatt-I7,
Koshy-5.13,
B&Q(2003)-Identity 33
F(4n) + 1 = F(2n−1) L(2n+1)
F(4n+1) + 1 = F(2n+1) L(2n)
F(4n+2) + 1 = F(2n+2) L(2n)
F(4n+3) + 1 = F(2n+1) L(2n+2)
 F(n)+1 is a product of a FIbonacci and a Lucas number:
A001611 F(n)+1, Formula by R K Guy (2003)
5 F(n) = L(n + 1) + L(n − 1)
L(n + 1)2 + L(n)2 = 5 F(2n + 1)Vajda-25a
L(n + 1)2 − L(n − 1)2 = 5 F(2n)-
L(n + 1)2 − 5 F(n)2 = L(2n + 1)-
L(2n) − 2 (−1)n = 5 F(n)2Vajda-23, Dunlap-25
L(n)2 − 4(−1)n = 5 F(n)2B&Q(2003)-Identity 53, Hoggatt-I12
F(n+k) + (−1)k F(n−k) = F(n)L(k)Bro U Alfred (1964), Bergum and Hoggatt (1975) equns (5),(7)
F(n+k) − (−1)k F(n−k) = L(n)F(k)Bro U Alfred (1964), Bergum and Hoggatt (1975) equns (6),(8)
L(n+k) + (−1)k L(n−k) = L(n)L(k)Bro U Alfred (1964), Bergum and Hoggatt (1975) equns (9),(11)
L(n+k) − (−1)k L(n−k) = 5F(n)F(k)Bro U Alfred (1964), Bergum and Hoggatt (1975) equns (10),(12)
F(n + 1) L(n) = F(2n + 1) + (−1)nVajda-30, Vajda-31,
Dunlap-27, Dunlap-30
L(n + 1) F(n) = F(2n + 1) − (−1)n-
F(2n + 1) = F(n + 1) L(n + 1) − F(n) L(n)Vajda-14, Dunlap-18
L(2n + 1) = F(n + 1) L(n + 1) + F(n) L(n)-
L(m) L(n) + L(m − 1) L(n − 1) = 5 F(m + n − 1) Hansen 1972
L(n)2 − 2 L(2n) = −5 F(n)2Vajda-22, Dunlap-24
5 F(n)2 − L(n)2 = 4 (−1)n + 1Vajda-24, Dunlap-26
F(n)2 + L(n)2 = 4 F(n + 1)2 − 2 F(2n)FQ (2003)vol 41, B-936, M A Rose, page 87
5 (F(n)2 + F(n + 1)2) = L(n)2 + L(n + 1)2Vajda-25
F(n) L(m) = F(n + m) + (−1)m F(n − m)a recurrence relation for F(n+km):
Vajda-15a, Dunlap-19
L(n) F(m) = F(n + m) − (−1)m F(n − m)Vajda-15b, Dunlap-20
5 F(m) F(n) = L(n + m) − (−1)m L(n − m)Vajda-17b, Dunlap-23, (special cases:Hoggatt-I16,I17)
2 F(n + m) = L(m) F(n) + L(n) F(m)Vajda-16a, Dunlap-2, FQ (1967) B106 H H Ferns pp 466-467
2 L(n + m) = L(m) L(n) + 5 F(n) F(m)FQ (1967) B106 H H Ferns pp 466-467
F(m) L(n) + F(m − 1) L(n − 1) = L(m + n − 1) Hansen (1972)
(−1)m 2 F(n − m) = L(m) F(n) − L(n) F(m)Vajda-16b, Dunlap-22
L(n + i) F(n + k) − L(n) F(n + i + k) =
(−1)n + 1 F(i) L(k)		Vajda-19a
F(n + i) L(n + k) − F(n) L(n + i + k) = (−1)n F(i) L(k)Vajda-19b
L(n + k + 1)2 + L(n − k)2 = 5 F(2n + 1)F(2k + 1) Melham (1999) Theorem 1
L(n + i) L(n + k) − L(n) L(n + i + k)
= (−1)n + 1 5 F(i) F(k)		Vajda-20b
(−1)kF(n)F(m−k) + (−1)mF(k)F(n−m) + (−1)nF(m)F(k−n) = 0 FQ 11 (1973) B228 page 108
(−1)kL(n)F(m−k) + (−1)mL(k)F(n−m) + (−1)nL(m)F(k−n) = 0 FQ 11 (1973) B229 page 108
5 F(jk+r) F(ju+v) = L(j(k+u)+(r+v)) - (-1)ju+vL(j(k-u)+(r-v)) Hansen (1978)
F(jk+r) L(ju+v) = F(j(k+u)+(r+v)) + (-1)ju+vF(j(k-u)+(r-v)) Hansen (1978)
L(jk+r) L(ju+v) = L(j(k+u)+(r+v)) + (-1)ju+vL(j(k-u)+(r-v)) Hansen (1978)
5F(a)F(b) − L(c)L(d) = (−1)r( 5F(a − r)F(b − r) − L(c − r)L(d − r) )
a+b=c+d for any integers a,b,c,d,r		 Johnson
F(a) L(b) − F(c) L(d) = (−1)r( F(a−r) L(b−r) − F(c−r) L(d−r)
with a+b=c+d		 Johnson-32, special case of Johnson-44

Higher Order Fibonacci and Lucas

Fibonacci and Lucas cubed

F(3n) = F(n + 1)3 + F(n)3 − F(n − 1)3 Lucas (1876), B&Q(2003)-Identity 232
5 L(3n) = L(n + 1)3 + L(n)3 − 3 L(n − 1)3 Long (1986) equation (45)
3 F(3n) = F(n+2)3 − 3 F(n)3 + F(n−2)3 J Ginsburg "A Relationship Between Cubes
of Fibonacci Numbers." Scripta Mathematica (1953) page 242.
L(3n) = L(n+1)F(n+1)2 + L(n)F(n)2 − L(n-2)F(n-1)2) Long (1986) equation (43)
5 F(3n) = F(n+1)L(n+1)2 + F(n)L(n)2 − F(n-1)L(n-1)2 Long (1986) equation (44)
F(n + 1)F(n + 2)F(n + 6) − F(n + 3)3 = (−1)nF(n)
F(n)F(n + 4)F(n + 5) − F(n + 3)3 = (−1)n+1F(n + 6) 		FQ 41 (2003) pg 142, Melham.
The second is a variant with -n for n and using Vajda-2
F(n−2)F(n−1)F(n+3) − F(n)3 = (−1)n-1F(n−3)
F(n+2)F(n+1)F(n−3) − F(n)3 = (−1)nF(n+3) 		Fairgrieve and Gould (2005)
versions of the above two formulae of Melham
F(n−2)F(n+1)2 − F(n)3 = (−1)n-1 F(n−1)
F(n+2)F(n−1)2 − F(n)3 = (−1)n F(n+1) 		Fairgrieve and Gould (2005)
F(n+a+b)F(n−a)F(n−b) − F(n-a-b)F(n+a)F(n+b)
= (−1)n+a+bF(a)F(b)F(a+b)L(n) 		Melham (2011) Theorem 1
F(n+a+b−c)F(n−a+c)F(n−b+c) − F(n−a−b+c)F(n+a)F(n+b)
= (−1)n+a+b+cF(a+b−c)( F(c)F(n+a+b−c) + (−1)cF(a−c)F(b−c)L(n) ) 		Melham (2011) Theorem 5
F(i+j+k) =
F(i+1)F(j+1)F(k+1) + F(i)F(j)F(k) − F(i−1)F(j−1)F(k−1)
for any integers i,j,k 		Johnson's (6)
F(3n) = F(n+1)3 + F(n)3 − F(n−1)3From Johnson's (6) with i=j=k
F(n)3 = F(n−1)3 + F(n−2)3 + 3 F(n)F(n−1)F(n−2) G Gelatti (2020, private communication)
L(5n) = L(n) (L(2n) + 5F(n) + 3)( L(2n) − 5F(n) + 3), n odd Aurifeuille's Identity (1879)
FQ 42 (2004) R S Melham, pgs 155-160

Fibonacci and Lucas to the fourth

F(4n) = F(n+1)4 + 2F(n)4 − F(n−1)4 + 4F(n)3F(n−1) Khomovsky (2018) A42
F(n−1)2F(n+1)2 − F(n−2)2F(n+2)2 = 4(−1)nF(n)2 Melham (2011) 21
F(n−3)F(n−1)F(n+1)F(n+3) − F(n)4 = (−1)nL(n)2 Melham (2011) 22
F(n)2 F(m + 1) F(m − 1) − F(m)2 F(n + 1) F(n − 1)
= (−1)n − 1 F(m + n) F(m − n)		Vajda-32
F(n − 2)F(n − 1)F(n + 1)F(n + 2) + 1 = F(n)4 Gelin-Cesàro Identity (1880) (see Dickson page 401)
FQ 41 (2003) pg 142, B&Q(2003)-Identity 31
Hoggatt-I29, Simson(1753)
L(n − 2)L(n − 1)L(n + 1)L(n + 2) + 25 = L(n)4B&Q(2003)-Identity 56
F(n+a+b+c)F(n−a)F(n−b)F(n−c) − F(n-a-b-c)F(n+a)F(n+b)F(n+c)
= (−1)n+a+b+cF(a+b)F(a+c)F(b+c)F(2n) 		Melham (2011) Theorem 2
F(n+a+b+c−d)F(n−a+d)F(n−b+d)F(n−c+d)
− F(n−a−b−c+2d)F(n+a)F(n+b)F(n+c)
= (−1)n+a+b+cF(a+b−d)F(a+c−d)F(b+c−d)F(2n+d)		 Melham (2011) Theorem 6
( F(n-1)F(n+2) )2 + (2 F(n)F(n+1) )2
= (F(n+1)F(n+2) − F(n-1)F(n))2
= F(2n+1)2		 A F Horadam FQ 20 (1982) pgs 121-122, B&Q(2003)-Identity 19 (corrected)
special case of Generalised Fibonacci Pythagorean Triples
( F(n)2 + F(n+1)2 + F(n+2)2 )2
= 2 ( F(n)4 + F(n+1)4 + F(n+2)4 ) 		Candido's Identity (1951)
FQ 42 (2004) R S Melham, pgs 155-160
( L(n-1)L(n+2) )2 + ( 2L(n)L(n+1) )2
= ( 5F(2n+1) ) 2		 Wulczyn FQ 18 (1980) pg 188
special case of Generalised Fibonacci Pythagorean Triples

Fibonacci and Lucas Higher Powers

F(5n) = F(n+1)5 + 4F(n)5 − F(n-1)5 + 10F(n+1)F(n)3F(n−1) Falcon, Plaza (2007)
F(n)F(n+1)F(n+2)F(n+4)F(n+5)F(n+6) + L(n+3)2
= ( F(n+3)( 2F(n+2)F(n+4) − F(n+3)2) )2		 Morgado (1987)
(
L(n) + √5 F(n)
2
 ) k  = 
L(kn) + √5 F(kn)
2
De Moivre Analogue,
S Fisk (1963) FQ 1.2 Problem B-10, pg 85.
Hoggatt-I44

Fibonomial formulae

The Fibonomials are defined using Fibonacci numbers instead of integers in binomial coefficients and Fibonacci factorials instead of normal factorials. There are many analagous results to those using binomial coefficients but using Fibonomials instead.

We define F!(n) = F(n)F(n-1)...F(2)F(1), n>0; F!(0)=1 for which some authors use n!F, to compare with n! = n(n-1)...3.2.1.
There is no universal notation for the Fibonomial. The fibonomial "Fibonacci n choose k" is defined as:

(n)F
k
   = 
F!(n)
F!(k) F!(n − k)
   =  
F(n)F(n−1)...F(n−k+1) F(n−k)F(n−k−1)...F(2)F(1)
F(k)F(k−1)...F(2)F(1)   F(n−k)F(n−k−1)...F(2)F(1)
   if n ≥ k ≥ 0
  = 0, otherwise
Vajda (page 74) uses J(n,k). D Knuth and others use double brackets:
((n))
k
while Melham (1999) and others use square brackets:
[
n
k
 ]

A simple alternative is to write fibonomial(n,k).
Here is a table of some values of the fibonomial (A010048)
n k 0 1 2 3 4 5 6 7
01
1 1 1
2 1 1 1
3 1 2 2 1
4 1 3 6 3 1
5 1 5 15 15 5 1
6 1 8 40 60 40 8 1
7 1 13 104 260 260 104 13 1
(
m + n
n
 ) F   =  F(m − 1) (
m + n − 1
n−1
 ) F + F(n + 1) (
m + n − 1
n
 ) F
Vajda page 74,
"add the two numbers above" analogy from Pascal's triangle
m
∑
j = 0
 (-1)j(j+3)/2
(m)F
j
 F(n+m−j)m+1 = F!(m) F((m+1)n+m(m+1) /2))
Melham (1999)....
1 F(n+1)2 + 1 F(n)2 = 1 F(2n+1)
1 F(n+2)3 + 1 F(n+1)3 −1 F(n)3 = 1.1 F(3n+3)
1 F(n+3)4 + 2 F(n+2)4 −2 F(n+1)4 − 1 F(n)4 = 1.1.2 F(4n+6)
1 F(n+4)5 + 3 F(n+3)5 −6 F(n+2)5 −3 F(n+1)5 + 1 F(n)5 = 1.1.2.3 F(5n+10)
1 F(n+5)6 + 5 F(n+4)6 −15 F(n+3)6 −15 F(n+2)6 + 5 F(n+1)6 + 1 F(n)6 = 1.1.2.3.5 F(6n+15)
 .... examples
0 = F(n) − F(n−1) − F(n−2)
0 = F(n)2 − 2 F(n−1)2 − 2 F(n−2)2 + F(n−3)2
0 = F(n)3 − 3 F(n−1)3 − 6 F(n−2)3 + 3 F(n−3)3 + F(n−4)3
0 = F(n)4 − 5 F(n−1)4 − 15 F(n−2)4 + 15 F(n−3)4 + 5 F(n−4)4 − F(n−5)4
...		Brousseau (1968)...but the general formula was not given.
For this see next line:
p
∑
k=0
(p)F
k
(−1)⌈k/2⌉F(n − k)p−1
 = 0, if p>0
 Knuth AoCP Vol 1 section 1.2.8 Exercise 30, (1997)
F(k)
(n)F
k
    =  
F( n − k + 1)
(n)F
k − 1
compare with
(n)
k
   =  
n − k + 1
k
(n)
k − 1
F(k)
(n)F
k
    =  
F( n )
(n − 1)F
k − 1
compare with
k
(n)
k
   =   n
(n − 1)
k − 1
F(n − k)
(n)F
k
   =  F( n )
(n − 1)F
k
compare with
n − k
(n)
k
   =  n
(n − 1)
k
(n)F
k
( k )F
j
   =  
( n )F
j
( n − j )F
k − j
compare with
(n)
k
( k )
j
   =  
( n )
j
( n − j )
k − j

G Formulae

G(i) is the General Fibonacci series. It has the same recurrence relation as Fibonacci and Lucas, namely G(n+2) = G(n+1) + G(n) for all integers n (i.e. n can be negative) Vajda-3,Dunlap 4, but the "starting values" of G(0)=a and G(1)=b can be specified. To make it clear which starting values for G(0)=a and G(1)=b are being used, we write G(a,b,i) for G(i). G(n) is an abbreviation for G(a,b,n) when a and b are understood from the context.
Special cases are the Fibonacci and Lucas series since F(n) = G(0,1,n) and L(n)=G(2,1,n):

Basic G Formulae

Two independent G series are here denoted G(n) and H(n), i.e. G(0) and G(1) are independent of H(0) and H(1).
G(n) = G(0) F(n − 1) + G(1) F(n)B&Q(2003)-Identity 37
G(−n) = (−1)n (G(0) F(n + 1) − G(1) F(n))ditto - applying Vajda-2 or
Vajda-9 with n=0
√5 G(n) = ( G(0) phi + G(1) ) Phin + (G(0) Phi − G(1)) ( −phi )n Vajda-55/56, Dunlap-77, B&Q(2003)-Identity 244
F(n) =
G(0) G(n+1) − G(1) G(n)
G(0)G(2) − G(1)2
Amer Math Monthly (2005) "Fibonacci, Chebyshev and
Orthogonal Polynomials"
D Aharonov, A Beardam, K Driver, p612-630
2 G(k) = ( 2 G(1) − G(0) ) F(k) + G(0) L(k) Johnson-46
G(n + m) = F(m − 1) G(n) + F(m) G(n + 1)Vajda-8, Dunlap-33, B&Q(2003)-Identity 38,
Johnson-40
G(n − m) = (−1)m (F(m + 1) G(n) − F(m) G(n + 1))Vajda-9, Dunlap-34, B&Q(2003)-Identity 47
G(n + m) + (−1)m G(n − m) = L(m) G(n) Vajda-10a, Dunlap-35, B&Q(2003)-Identity 45,
Bergum & Hoggatt (1975) (36) and (38)
G(n + m) − (−1)m G(n − m) = F(m) ( G(n−1) + G(n+1)) Vajda-10b, Dunlap-36, B&Q(2003)-Identity 48,
Bergum & Hoggatt (1975) (37) and (39)
G(m) F(n) − G(n) F(m) = (−1)n+1 G(0) F(m − n)Vajda-21a
G(m) F(n) − G(n) F(m) = (−1)m G(0) F(n − m)Vajda-21b
G(m+k) F(n+k) + (−1)k+1 G(m) F(n) = F(k) G(m + n + k)Howard(2003)

G Formulae of Order 2 or more

These formulae include terms which are a product of two G numbers either from the same G series of from two different G series i.e. with different index 0 and 1 values. Where the series may be different they are denoted G and H e.g. special cases include G = F (i.e. Fibonacci) and H = L (i.e. Lucas), or they could also be the same series G=H.
G(n + i) H(n + k) − G(n) H(n + i + k)
= (−1)n (G(i) H(k) − G(0) H(i + k))		 Vajda-18 (corrected), B&Q(2003)-Identity 44 (also Identity 68)
a special case of Johnson-44:
G(p)H(q) − G(r)H(s)
= (-1)n[ G(p-n)H(q-n) − G(r-n)H(s-n) ]
if p+q = r+s and p,q,r,s,n are integers		 Johnson-44
G(n + 1) G(n − 1) − G(n)2 = (−1)n (G(1)2 − G(0) G(2)) Vajda-28, B&Q(2003)-Identity 46
4 G(n−1)G(n) + G(n−2)2 = G(n+1)2B&Q(2003)-Identity 65
G(n + 3)2 + G(n)2 = 2( G(n+1)2 + G(n+2)2 ) B&Q(2003)-Identity 70
G(i+j+k) = F(i+1)F(j+1)G(k+1) + F(i)F(j)G(k) − F(i−1)F(j−1)G(k−1)
for any integers i,j,k 		Johnson (39a)
4G(i)2G(i+1)2 + G(i−1)2G(i+2)2 = ( G(i)2 + G(i+1)2 )2Generalised Fibonacci Pythagorean Triples
Horadam (1967)
G(n + 2)G(n + 1)G(n − 1)G(n − 2) + ( G(2)G(0) − G(1)2 )2
= G(n)4		 B&Q(2003)-Identity 59

Summations

This section has formulae that sum a variable number of terms.

Fibonacci and Lucas Summations

These formulae involve a sum of Fibonacci or Lucas numbers only.
n
∑
i = 0
 F(i) = F(n + 2) − 1
 Hoggatt-I1, Lucas(1878), B&Q 2003-Identity 1
n
∑
i = 0
 (-1) i F(i) = (-1)n F(n − 1) − 1
 B&Q 2003-Identity 21
n
∑
i = 0
 L(i) = L(n + 2) − 1
 Hoggatt-I2
n
∑
i = a
 F(i) = F(n + 2) − F(a + 1)
 -
n
∑
i = a
 L(i) = L(n + 2) − L(a + 1)
 -
n
∑
i = 0
 F(2i) = F(2n + 1) − 1, n≥0
 Hoggatt-I6, Lucas(1878), B&Q(2003)-Identity 12
n
∑
i = 1
 F(2i − 1) = F(2n), n≥1
 Hoggatt-I5, Lucas(1878), B&Q(2003)-Identity 2
n
∑
i = 1
 L(2i − 1) = L(2n) − 2
-
n
∑
i = 1
  2n − i F(i − 1) = 2n  − F(n + 2)
 Vajda-37a(adapted),
Dunlap-42(adapted),
B&Q(2003)-Identity 10
n
∑
i = 0
  2i L(i) = 2n+1 F(n + 1)
 B&Q(2003)-Identity 236
n
∑
i = 0
F(3i + 1)
 =
F(3n + 3)
2
B&Q(2003)-Identity 23
n
∑
i = 0
F(3i + 2)
 =
F(3n + 4) − 1
2
B&Q(2003)-Identity 24 (corrected)
n
∑
i = 0
F(3i)
 =
F(3n + 2) − 1
2
B&Q(2003)-Identity 25 (corrected)
n
∑
i = 0
 F(4i) = F(2n + 1)2 − 1
 B&Q 2003-Identity 27
n
∑
i = 0
 F(4i + 1) = F(2n + 1)F(2n + 2)
B&Q 2003-Identity 26
n
∑
i = 0
 F(4i + 2) = F(2n + 1)F(2n + 3) − 1
 B&Q 2003-Identity 29
n
∑
i = 0
 F(4 i + 3) = F(2n + 3)F(2n + 2)
 B&Q 2003-Identity 28
n
∑
i = 0
 (−1)i L(n − 2i) = 2 F(n + 1)
Vajda-97, Dunlap-54
n
∑
i = 0
 (−1)i L(2n − 2i + 1) = F(2 n + 2)
B&Q(2003)-Identity 55

Decimal (and other bases) fractions

We saw in The Fibonacci Series as a Decimal Fraction that the Fibonacci series occurs naturally as the decimal expansion of a simple fraction in several ways:
1/89 = 0.0 1 1 2 3 5 ...
1/9899=0.00 01 01 02 03 05 08 13 21 ...
with a varying number of decimal digits before the Fibonacci numbers overlap and the series is obscured. This section gives formulae for these fractions for various subsequences of Fibonacci and General Fibonacci series.
∞
∑
k = 1
 10−n(k+1)F(ak)
=
F(a)
102n − 10nL(a) − (−1)a
Hudson and Winans (1981)
If P(n) = a P(n-1) + b P(n-2) for n≥2; P(0) = c; P(1) = d and
m and N are defined by B2 = m + Ba + b, N = cm + dB + bc,
then
 N 
Bm		  = 
∞
∑ 
i = 1
P(i−1)
Bi

provided that |(a+√(a2+4b))/(2B)| < 1 and
| (a−√(a2+4b))/(2B) | < 1 		Long (1981)

Summations with fractions

∞
∑
i = 0
F(i)
--
2i
  = 2
 Vajda-60, Dunlap-51
∞
∑
i = 0
L(i)
--
2i
  = 6
 -
∞
∑
i = 0
F(i)
--
ri
 =
r
--
r2 − r − 1
-
∞
∑
i = 0
L(i)
--
ri
 = 2 +
r +2
--
r2 − r − 1
-
∞
∑
i = 1
i F(i)
--
2i
  = 10
 Vajda-61, Dunlap-52
∞
∑
i = 1
i L(i)
--
2i
  = 22
 -
∞
∑
i = 0
1
--
F(2i)
  = 4 − Phi = 3 − phi
 Vajda-77(corrected), Dunlap-53(corrected)
n
∑
i = 1
(−1)2i-1r
--
F(2ir)
 =
(−1)r F( r(2n−1) )
--
F(r) F(2n r)
Vajda-89 (corrected)
 
∑ 
k ≥ 2
1
--
F(k−1)F(k+1)
  = 1
 R L Graham (1963) FQ 1.1, Problem B-9, pg 85, FQ 1.4 page 79
 
∑ 
k ≥ 2
F(k)
--
F(k−1)F(k+1)
  = 2
 R L Graham (1963) FQ 1.1, Problem B-9, pg 85
 
∑ 
k ≥ 2
(−1)k
--
F(k)F(k−1)
  = phi
 Johnson-11, Vajda-102

Order 2 summations

n
∑
i = 1
 F(i)2 = F(n) F(n + 1)
Vajda-45, Dunlap-5,
Hoggatt-I3, Lucas(1878),
Koshy-77,
B&Q(2003)-Identity 9 (Identity 233 variant)
n
∑
i = 1
 L(i)2 = L(n) L(n + 1) − 2
 Hoggatt-I4
2n-1
∑
i = 0
 L(i)2 = 5 F(2n) F(2n - 1)
-
2n
∑
i = 1
 F(i) F(i − 1) = F(2n)2
Vajda-40, Dunlap-45
2n
∑
i = 1
 L(i) L(i − 1) = L(2n)2 − 4
 -
2n+1
∑
i = 1
 F(i) F(i − 1) = F(2n +1)2 − 1
 Vajda-42, Dunlap-47
2n+1
∑
i = 1
 L(i) L(i − 1) = L(2n +1)2 − 1
 -
5 n
∑
k = 0
 (−1)r(1+k) F(r(1+k))2 = (−1)r(n+1)
F((2n+3)r)
F(r)
   − 2n − 3
 Vajda-93
n
∑
k = 0
 (−1)r(1+k) L(r(1+k))2 = (−1)r(n+1)
F((2n+3)r)
F(r)
   + 2n + 1
 Vajda-94
n−1
∑
i=0
 F(2i + 1)2 =
F(4n) + 2n
5
 Vajda-95, B&Q(2003)-Identity 234
n
∑
i=0
 F(2i)2 =
F(4n + 2) − 2n − 1
5
 Vajda page 70
n−1
∑
i = 0
 L(2i + 1)2 = F(4n) − 2n
 Vajda-96, B&Q(2003)-Identity 54
n
∑
i = 1
 L(2i)2 = F(4n + 2) + 2n − 1
 Vajda page 70
5
n
∑
i = 0
 F(i) F(n − i)
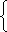{ = (n + 1) L(n) − 2 F(n + 1)
= n L(n) − F(n)
 Vajda-98, Dunlap-55, B&Q(2003)-Identity 58
n
∑
i = 0
 L(i) L(n − i)
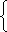{ = (n + 1) L(n) + 2 F(n + 1)
= (n + 2) L(n) + F(n)
 Vajda-99, Dunlap-56, B&Q(2003)-Identity 57
n
∑
i = 0
 F(i) L(n − i) = (n + 1) F(n)
 Vajda-100, Dunlap-57, B&Q(2003)-Identity 35
2n−1
∑
k = 1
 (2n − k) F(k)2 = F(2n)2
 V Hoggatt (1965) Problem B-53 FQ 3, pg 157

Summations of order > 2

10
n
∑
i = 1
 F(i)3 = F(3n+2) + 6(-1)n+1F(n−1) +5
adapted from Benjamin, Carnes, Cloitre (2009)
25
n
∑
i = 1
 F(i)4 = F(4n+2) + 4(-1)n+1F(2n + 1) +6n + 3
see A005969
4
n
∑
k = 1
 F(k)6 = F(n)5F(n+3) + F(2n)
Ohtsuka and Nakamura (2010) Theorem 1
4
n
∑
k = 1
 L(k)6 = L(n)5L(n+3) + 125 F(2n) − 128
 Ohtsuka and Nakamura (2010) Theorem 2

G Summations

Two independent G series are denoted G(n) and H(n).
n
∑
i = 1
 G(i) = G(n + 2) − G(2)
 L G Brökling (1964) FQ 2.1 Problem B-20 solution, pg76;
Vajda-33; Dunlap-38; B&Q(2003)-Identity 39
n
∑
i = a
 G(i) = G(n + 2) − G(a + 1)
 -
n
∑
i = 1
 G(2i − 1) = G(2n) − G(0)
 Vajda-34, Dunlap-37, B&Q(2003)-Identity 61
n
∑
i = 1
 G(2i) = G(2n + 1) − G(1)
 Vajda-35, Dunlap-39, B&Q(2003)-Identity 62
n
∑
i = 1
 G(2i) −
n
∑
i = 1
 G(2i − 1) =
2n
∑
i = 1
 (−1)iG(i) = G(2n − 1) + G(0) − G(1)
 Vajda-36, Dunlap-40
n
∑
k = 1
 G(k − 1) 2−k = ( G(0) + G(3) )/2 − G(n + 2) 2−n
 Vajda-37, Dunlap-41,
B&Q(2003)-Identity 69
4n+2
∑
i = 1
 G(i) = L(2n + 1) G(2n + 3)
 Vajda-38, Dunlap-43, B&Q(2003)-Identity 49
2n
∑
i = 1
 G(i) G(i − 1) = G(2n)2 − G(0)2
 Vajda-39, Dunlap-44, B&Q(2003)-Identity 41
2n+1
∑
i = 1
 G(i) G(i − 1) = G(2 n + 1)2 − G(0)2 − G(1)2 + G(0)G(2)
 Vajda-41, Dunlap-46
n
∑
i = 1
 G(i + 2) G(i − 1) = G(n + 1)2 − G(1)2
Vajda-43, Dunlap-48, B&Q(2003)-Identity 64
(1 + (−1)r − L(r) )
n
∑
k = 0
 G(m + kr) =
G(m) − G(m+(n+1)r) + (−1)r(G(m+nr) − G(m−r))
Fibonacci with a Golden Ring
Kung-Wei Yang Mathematics Magazine 70 (1997),
pp. 131-135.
n
∑
i = 1
 G(i)2 = G(n) G(n + 1) − G(0) G(1)
 Vajda-44, Dunlap-49, B&Q(2003)-Identity 67
∞
∑
i = 0
G(a, b, i)
ri
= a + a + b r
r2 − r − 1
 Stan Rabinowitz,
"Second-Order Linear Recurrences" card,
Generating Function
special case (x=1/r, P=1, Q=-1)
∞
∑
i = 0
i G(a, b, i)
ri
r (b r2 − 2 a r + b − a)
=
(r2 − r − 1)2
 -
2n − 1
∑
i = 1
G( i ) H( i )
 = G ( 2n ) H( 2n − 1) − G(0) H(1)
 B&Q(2003)-Identity 42

Summations with Binomial Coefficients

n
∑
i = 1
(n−i
i−1		)
 = F(n)
B&Q(2003) Identity-4
∞
∑
i = 0
(n−i−1
i		)
 = F(n)
Vajda-54(corrected),
Dunlap-84(corrected)
n
∑
i = 0
(n+i
2i		)
 = F(2n + 1)
B&Q(2003)-Identity 165
n−1
∑
i = 0
(n+i
2i+1		)
 = F(2n)
B&Q(2003)-Identity 166
n
∑
k = 0
(n
k		)
 F(k) = F(2n)
S Basin & V Ivanoff (1963) Problem B-4, FQ 1.1 pg 74, FQ1.2 pg 79; B&Q(2003)-Identity 6
n
∑
k = 0
(n
k		)
 (−1)k+1 F(k) = F(n)
I Ruggles (1963) FQ 1.2 pg 77
n
∑
k = 0
(n
k		)
 (−1)k L(k) = L(n)
I Ruggles (1963) FQ 1.2 pg 77
n
∑
k = 0
(n
k		)
 F(p−k) = F(p+n)
B&Q(2003)-Identity 20
n
∑
k = 1
(n
k		)
 2kF(k) = F(3n)
B&Q(2003)-Identity 238, Vajda-68, Griffiths (2013) 8-corrected
n
∑
k = 0
 (−1)n−k
(n
k		)
 2kF(2 k) = F(3 n)
Griffiths (2013) page 239-corrected
n
∑
k = 0
(n
k		)F(3k + m)
 = 2nF(2n + m)
Griffiths (2013)
n
∑
k = 0
 (−1)n−k
(n
k		)
 F(3 k) = 2n F(n)
Griffiths (2013) page 239
n
∑
i = 0
(n+1
i+1		)
 F(i) = F(2n + 1) − 1
Vajda-50, Dunlap-82
2n
∑
i = 0
(2n
i		)
 F(2i + p) = 5n F(2n + p)
Hoggatt-I41 (special case p=0: Vajda-69, Dunlap-85)
2n
∑
i = 0
(2n
i		)
 L(2i) = 5n L(2n)
Vajda-71, Dunlap-87
2n+1
∑
i = 0
(2n+1
i		)
 F(2i + p) = 5n L(2n + 1 + p)
Hoggatt-I42 (special case p=0: Vajda-70, Dunlap-86)
2n+1
∑
i = 0
(2n+1
i		)
 L(2i) = 5n + 1 F(2n + 1)
Vajda-72, Dunlap-88
2n
∑
i = 0
(2n
i		)
 F(i)2 = 5n − 1 L(2n)
Vajda-73, Dunlap-89,Hoggatt-I45
2n
∑
i = 0
(2n
i		)
 L(i)2 = 5n L(2n)
Vajda-75, Dunlap-91, Hoggatt-I46
2n+1
∑
i = 0
(2n+1
i		)
 F(i)2 = 5n F(2n + 1)
Vajda-74, Dunlap-90, Hoggatt-I47
2n+1
∑
i = 0
(2n+1
i		)
 L(i)2 = 5n + 1 F(2n + 1)
Vajda-76, Dunlap-92
∞
∑
i = 0
 5i 
(n
2i+1		)
  = 2n − 1 F(n)
 Vajda-91, B&Q(2003)-Identity 235, Catalan 1857
∞
∑
i = 0
 5i 
(n
2i		)
  = 2n − 1 L(n)
 Vajda-92, B&Q(2003)-Identity 237, Catalan (1857)-see Vajda pg 69
k
∑
i = 0
(k
i		)
 F(n)iF(n−1)k − iF(i) = F( kn )
Rabinowitz-17 (special case of Vajda-66)
k
∑
i = 0
(k
i		)
 F(n)iF(n−1)k − iL(i) = L( kn )
Rabinowitz-17 (special case of Vajda-66)
p
∑
i = 0
(p
i		)
 F(t)iF(t−1)p − iG( m+i ) = G( m+tp )
Vajda-66,B&Q(2003) Identity-11
 
∑
i ≥ 0
 
∑
j ≥ 0
(n − i
j		) (n − j
i		)
 = F( 2n + 3 )
B&Q(2003) Identity 5
F(r n)
F(r)
 =
[(n − 1)/2]
∑
k = 0
 (−1)k(r−1)
( n − k − 1
k		 )
 L(r)n − 1 − 2k
Lucas (1878) equations 74-76,
this form due to Hoggatt and Lindt (1969), see Gould (1977)
n
∑
k = 0
 (−1)k
(2n+1
k		)
 L(2n + 1 − 2k)  = 1
 Griffiths (2013)

Powers of Fibonacci and Lucas as Sums

5k/2 F(t)k =
(k−1)/2
∑
i = 0
(k
i		)
 (−1)i(t+1) √5 F( (k−2i)t ), k odd
Vajda-80
5k/2 F(t)k =
k/2 −1
∑
i = 0
(k
i		)
 (−1)i(t+1) L( (k−2i)t ) +
(k
k/2		)
 (−1)(t+1)k/2, k even
Vajda-81
L(t)k =
(k−1)/2
∑
i = 0
(k
i		)
 (−1)it L( (k−2i)t ) , k odd
Vajda-78
L(t)k =
k/2 −1
∑
i = 0
(k
i		)
 (−1)it L( (k−2i)t ) +
(k
k/2		)
 (−1)tk/2, k even
Vajda-79
Fk
m		F 
n		 = (−1)kr
 
k
∑
h = 0
 ( k
h		 ) (−1)h
 		 Fh
r		 Fk−h
r+m		 F 
n+kr+hm
On a General Fibonacci Identity
J H Halton, Fib Q, 3 (1965), pp 31-43

Summations with Binomials and G Series

n
∑
i = 0
(n
i		)
 G(i) = G(2n)
I Ruggles (1963) FQ 1.2 pg 77; Vajda-47; Dunlap-80
n
∑
i = 0
(n
i		)
 2i G(i) = G(3n)
B&Q(2003)-Identity 239
n
∑
i = 0
(n
i		)
 G(p − i) = G(p + n)
Vajda-46, Dunlap-79, B&Q(2003)-Identity 40
n
∑
i = 0
(n
i		)
 G(p + i) = G(p + 2n)
Vajda-49, Dunlap-81
p
∑
i = 0
 (−1)p−i
(p
i		)
 G( n+i ) = G( n−p )
Vajda-51, Dunlap-83

Products

n
F(n+1)  = 
F(n+2)
 ∏
1 −   (−1)k
F(k+1)2
 , n ≥ 0
k = 1
 B&Q(2003) Identity 22

Trigonometric Formulae

⌊(n-1)/2 ⌋
F(n) = ∏
3 + 2 cos  2kπ
n
 , n ≥ 1
k = 1
 D Lind, Problem H-93,
FQ 4 (1966), page 332
⌊(n-2)/2 ⌋
L(n) = ∏
3 + 2 cos  (2k+1)π
n
 , n ≥ 2
k = 0
 D Lind, Problem H-93, FQ 4 (1966),
page 252, corrected page 332

E and Logs

ln(x) = loge(x)
Here we use g for ln(Phi), the natural log of Phi so that cosh(g) = √5 / 2.
F( 2n ) = 2sinh( 2ng )
√5
from Binet's formula
         =  sinh( 2ng )
cosh( g )
F( 2n+1 ) = 2cosh( (2n+1)g )
√5
from Binet's formula
         =  cosh( (2n+1)g )
cosh( g )
L( 2n) = 2 cosh( ng )from Binet's formula
L( 2n+1 ) = 2 sinh( ng )from Binet's formula
∞
∑
k = 1
Φ F(k) − F(k+1)
k
= ∞
∑
k = 1
√5 F(k) − L(k)
2 k
 = g
 C. Brown (Jan 2016) private communication
∞
∑
n = 0
F(n)
--
n!
 =
eΦ − e−φ
√5
Exponential Generating Functions For Fibonacci Identities
C Church and Marjorie Bicknell, Fib Q vol 11 (1983) 275-281,with z=1
∞
∑
n = 0
L(n)
--
n!
 = eΦ + e−φ
Exponential Generating Functions For Fibonacci Identities
C Church and Marjorie Bicknell, Fib Q vol 11 (1983) 275-281,with z=1

Complex Numbers

i = √−1
sin( π/2 + i ln(Φ) ) = (√5)/2 = Φ + ½ Schroeder 1986, equation (5.41) page 68
F(n) =
n−1
∏
k = 1
( 1 − 2 i cos  k π
n		 )
D Lind, Problem H-64, FQ 3 (1965), page 116
F(n) = 2 i 1−n sin(−i n ln( i Phi) )
√5
 from Rabinowitz-7 corrected, using Phi2 = (√5 + 1)/(√5 − 1)
F(n) = 2 i −n sinh(n ln( i Phi) )
√5
 from Rabinowitz-7 corrected
L(n) = 2 i −n cos(−i n ln( i Phi) ) from Rabinowitz-7 corrected
L(n) = 2 i −n cosh( n ln( i Phi) ) from Rabinowitz-7 corrected
√1 + 2i = √Phi + i √phi
 
= [ 1 + i ;  2 + 2i  ]
 I J Good (1993)
√1 + i/2 = ( √ √5 + 2 + i √ √5 − 2  ) /2
= ( Phi3/2 + i phi3/2 ) /2
= [ 1 + i  ;  1 + i  ]
2
 I J Good (1993)

Generating Functions

This section is now part of the following reference page on Linear Recurrence Relations and Generating Functions

References

The Fibonacci Quarterly journal: all papers older than 7 years are freely available online as PDFs; those published within the last 7 years are only available online to subscribers.
Arranged in alphabetical order of author:

Previous Topic Fibonacci and Phi in the Arts Fib HOME Fibonacci Home Page Calculator

This is the first page on this Topic.

WHERE TO NOW???

Next Page Recurrence Relations & Generating Functions


More topics at Ron Knott's Home page

Valid HTML 4.01! © 1996-2021 Dr Ron Knott
The URL of this document is
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibFormulae.html